3.9 and 3.11 Deveoping Algorithms/Binary Search

• Notes
• Vocab
• Hacks 3.9.1
  • 1
• Hacks for 3.9.2
  • Natural lang
• Hacks 3.9.3
• Hacks 3.11

Notes

• If code look the same i doesn't mean it does the same thin
• Note what code
• Before making an agorthim plan out all steps
• Outline can be made with flow charts or just write them out

Vocab

• Binary Search: repeatedly dividing a search interval in half

Hacks 3.9.1

1

• It is imporant because different algorithms can output different things ## 2

isRaining = True
isSunny = False

#If Statements
if isRaining == True:
    print("Get an umbrella for the walk")
else:
    print("Go on a Walk")

if isSunny == True:
    print("Go on a walk :)")

Get an umbrella for the walk

isRaining = False
isSunny = True

# Setting Var
goforWalk = isRaining or not(isSunny)

# If statements
if goforWalk == False:
    print("don't walk")
else:
    print("go for a walk")

don't walk

Hacks for 3.9.2

Natural lang

• Start
• Are you old enought to drink
• if not wait a year
• do you have money
• if not you're poor
• if so you get beer

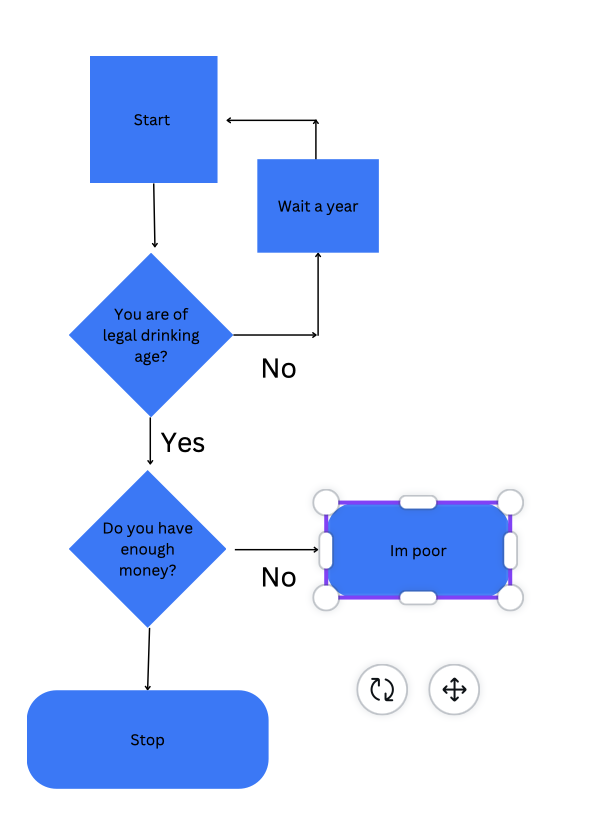
age = 17
money = 4
#When they are under age they wait a year until they are over
while age <= 20:
    age = age + 1
    print(age)
if age >= 21:
    if money >= 3.99:
        print("Here is your Drink")
        #if they don't have enough money they will say they are poor
    else:
        print("im poor")

Hacks 3.9.3

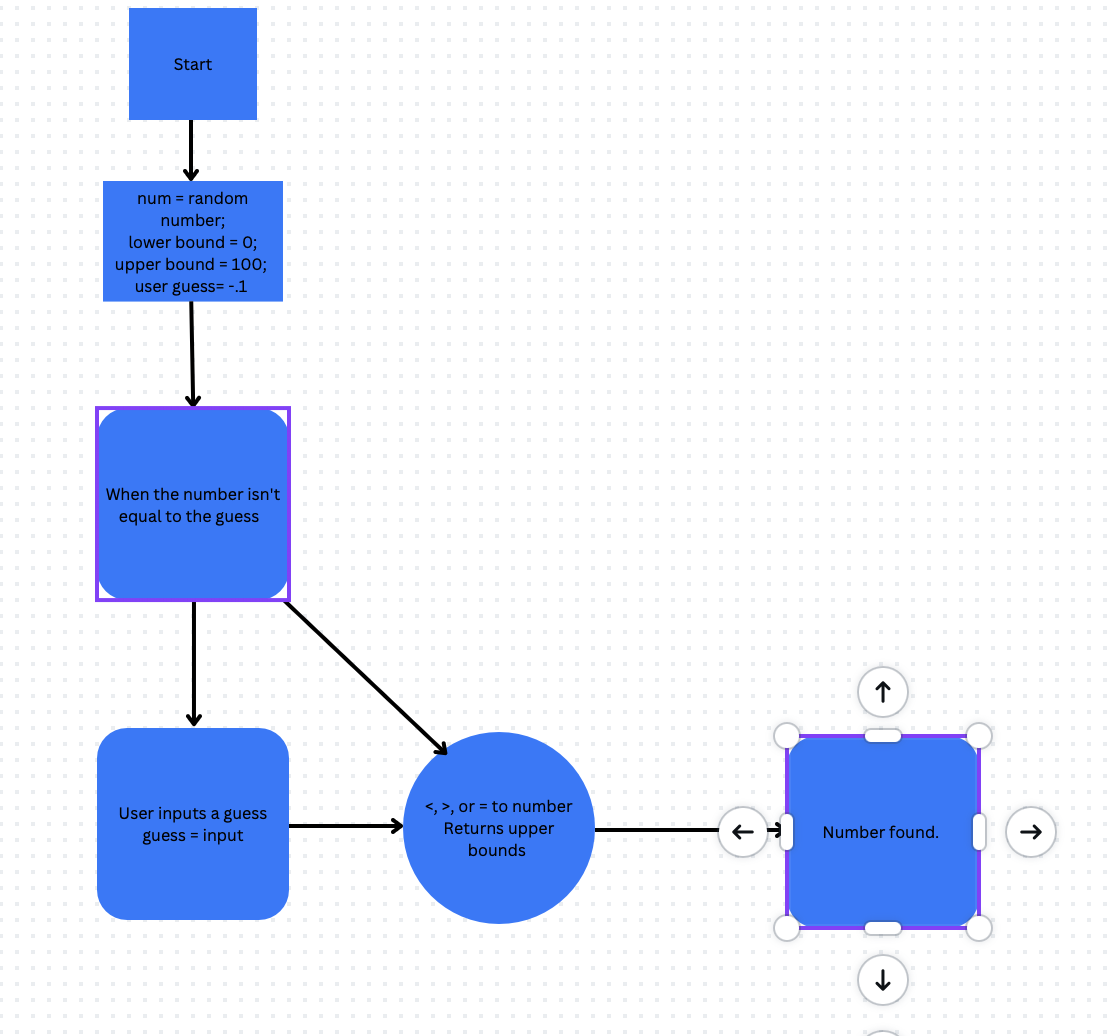
import random

#sets variables for the game
num_guesses = 0
user_guess = 0
upper_bound = 100
lower_bound = 0

#generates a random number
number = random.randint(1,100)

# print(number)     #for testing purposes
print(number)
print("I'm thinking of a number between 1 and 100.")

#Write a function that gets a guess from the user using input()
def guess():
    g = int(input("Choose a number"))
    return g #add something here 

#Change the print statements to give feedback on whether the player guessed too high or too low
def search(number, guess):
    global lower_bound, upper_bound
    if guess < number:
        print("Higher, your getting there") #change this
        lower_bound = guess
    elif guess > number:
        print("Lower, your getting closer") #change this
        upper_bound = guess
    return lower_bound, upper_bound

while user_guess != number:
    user_guess = guess()
    num_guesses += 1
    print(f"You guessed {user_guess}.")
    lower_bound, upper_bound = search(number, user_guess)
    print(f"Guess a number between {lower_bound} and {upper_bound}.")

print(f"You guessed the number in {num_guesses} guesses!")

72
I'm thinking of a number between 1 and 100.
You guessed 50.
Higher
Guess a number between 50 and 100.
You guessed 72.
Guess a number between 50 and 100.
You guessed the number in 2 guesses!

Hacks 3.11

numlist1 = [12, 14, 43, 57, 79, 80, 99]
numlist2 = [92, 43, 74, 66, 30, 12, 1]
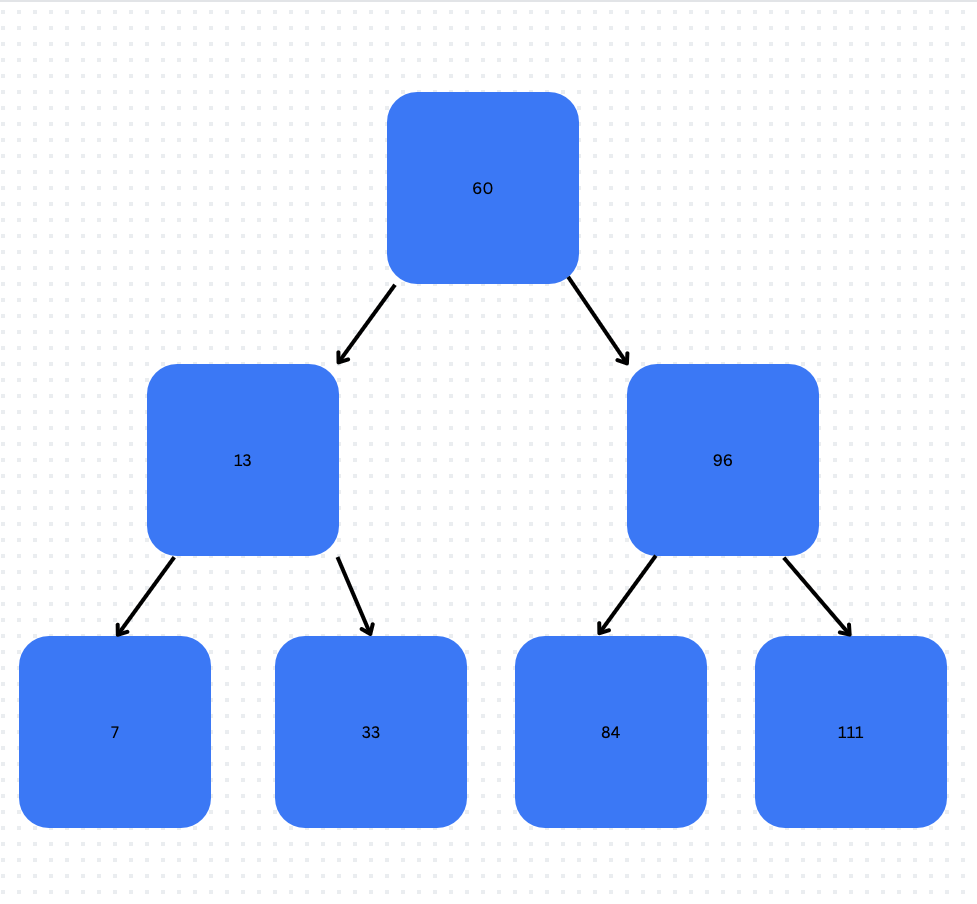
numlist3 = [7, 13, 96, 111, 33, 84, 60]

def middle(x):
    y = (7+1)/2
    middle = x[int(y)]
    return middle

x = numlist1
print(middle(x))

79

• The Second number would be looked at more because binary starts at 1
• [3, 2, 8, 12, 99] can not be searched because the order of the numbers is not perfect